

Hello, I'm

Hello, I'm
Get To Know More

SciML and Applied AI Research

BA Physics, Computer Science and Economics
Hello! I'm Maxim Beekenkamp a senior at Brown University studying Physics, Computer Science and Economics.
Motivated by my personal journey as well as my research background, I'm interested in the intersection of
Scientific Machine Learning (SciML) and applied AI research.
Diving into the varied AI applications in my degrees (Physics, Computer Science and Economics) has energised my academic experience.
This interdisciplinary approach to AI research has enabled me to apply insights from diverse fields,
fostering both creative problem solving abilities and comprehensive understanding of the ethical and societal implications of AI advancement.
allowing me to harness insights from different disciplines whilst providing a holistic perspective into the social responsibilities associated with developing AI.
I’ve thrived in collaborative environments whilst researching novel AI techniques to unlock insights in the natural sciences or applying deep learning frameworks to finance,
where my passion for crafting impactful solutions in a diverse and inclusive team has remained a cornerstone of my personal ethos, consistently demonstrated in my collaborative work.
Whilst at Brown University, I have been working on multiple projects with
The Crunch Group focusing on physics informed neural networks and deep operator networks. Prior to this position as an undergraduate research assistant,
I have worked in at ML42 Partners where I applied this same passion for AI research to the financial sector.
Regardless of the setting I have consistently engaged with AI, whether in a lab, corporate environment or in my personal projects.


Explore My










Browse My Recent
Won UTRA Award for research “Generalizing AI for Partial Differential Equations:
A Path towards AGI” during the summer of 2023.
Designed a DeepONet to learn Darcy's equation, and iterated on the architecture
(Adaptive DeepONets) to effectively incorporate transfer learning goals and solve
across multiple geometries, initial and boundary conditions.
Implemented an algorithm to adaptively select the most ‘important’ nodes and prune
‘unimportant’ ones which created space in the neural network to learn the features
of new geometries or conditions. This allows transfer learning to occur whilst circumventing
catastrophic forgetting.
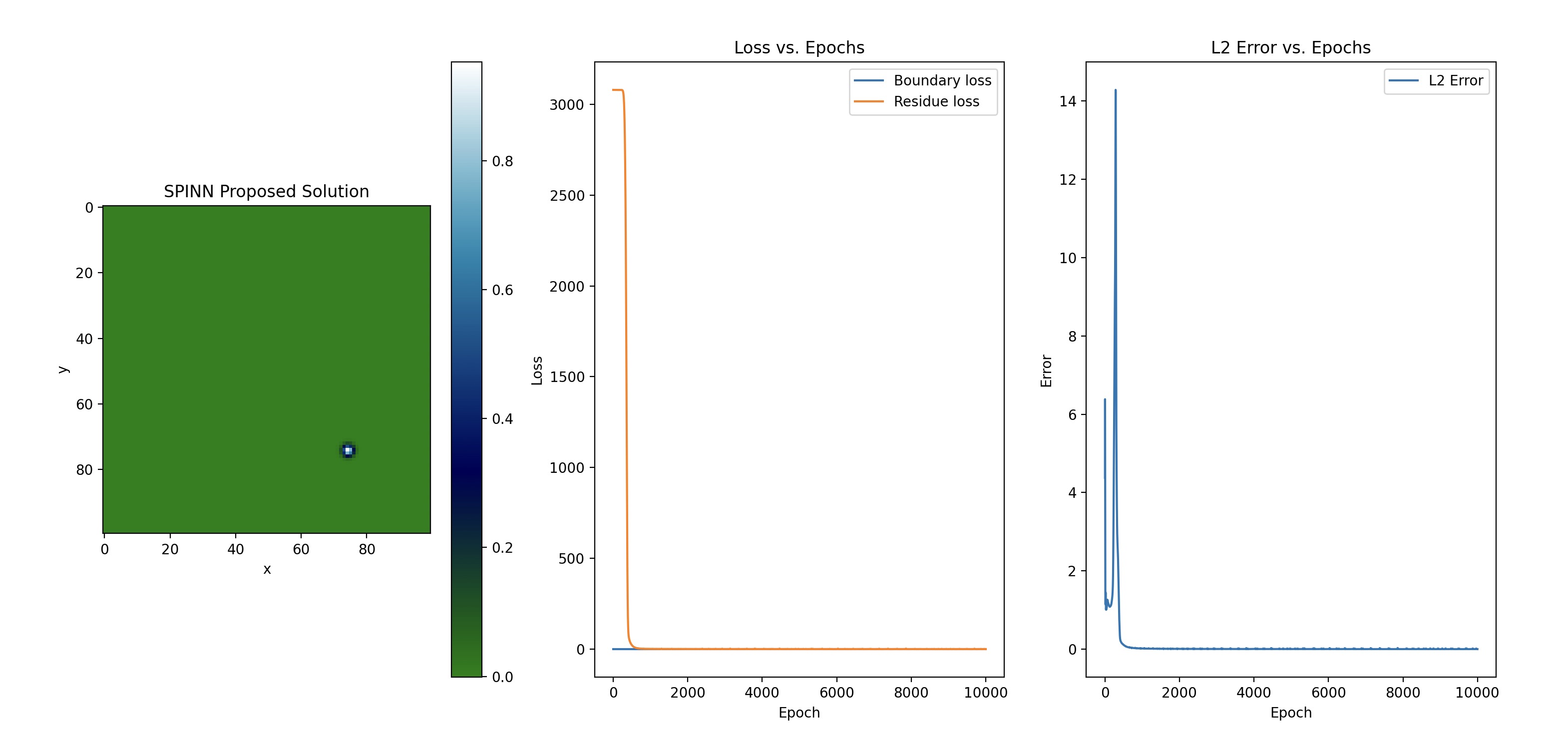
A separable and self-adaptive neural network, solving a two-dimensional time-dependent
heat equation using JAX.
Leveraged low-rank decomposition using forward-mode autodifferentiation to operate on a
per-axis basis which reduced the L2 error of a conventional PINN by 3 orders of magnitude
whilst simultaneously decreasing the per iteration runtime of a conventional PINN by 96.5%.
Implemented in two weeks before the theorised code was released.
A self-adaptive neural network using JAX. Providing a solution with an L2 error on the order of e-4.
The self-adaptive loss weighting balances the gradient updates to most effectively learn both the boundary
and residual errors. Improved L2 error at boundary conditions 6 orders of magnitude compared to conventional
PINNs whilst having a negligible impact on runtime.
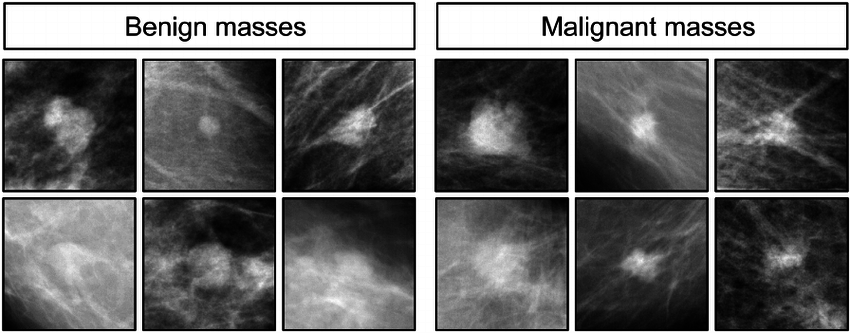
A deep learning classifier for the Breast Cancer Wisconsin (Diagnostic) dataset consisting of a fine needle aspirate images.
Correctly assigns labels representing the diagnosis (benign or malignant) 96.5% of the time.
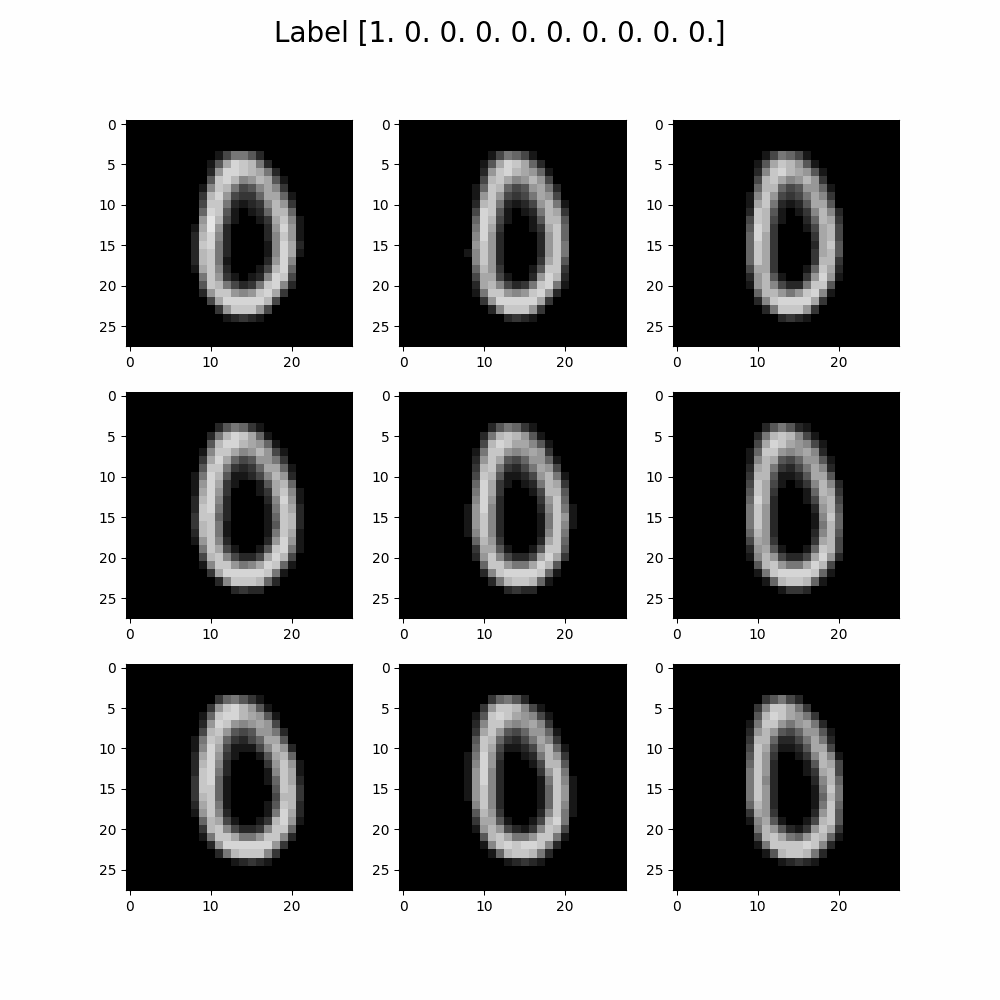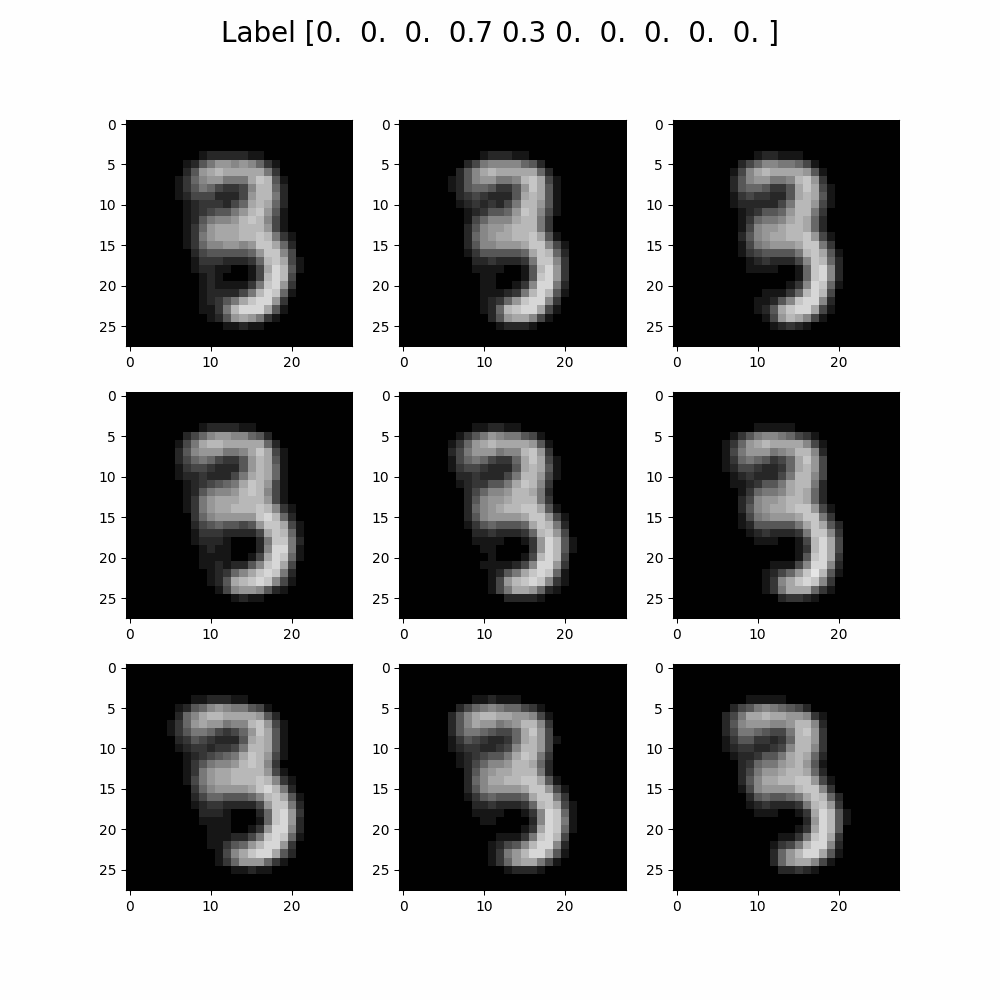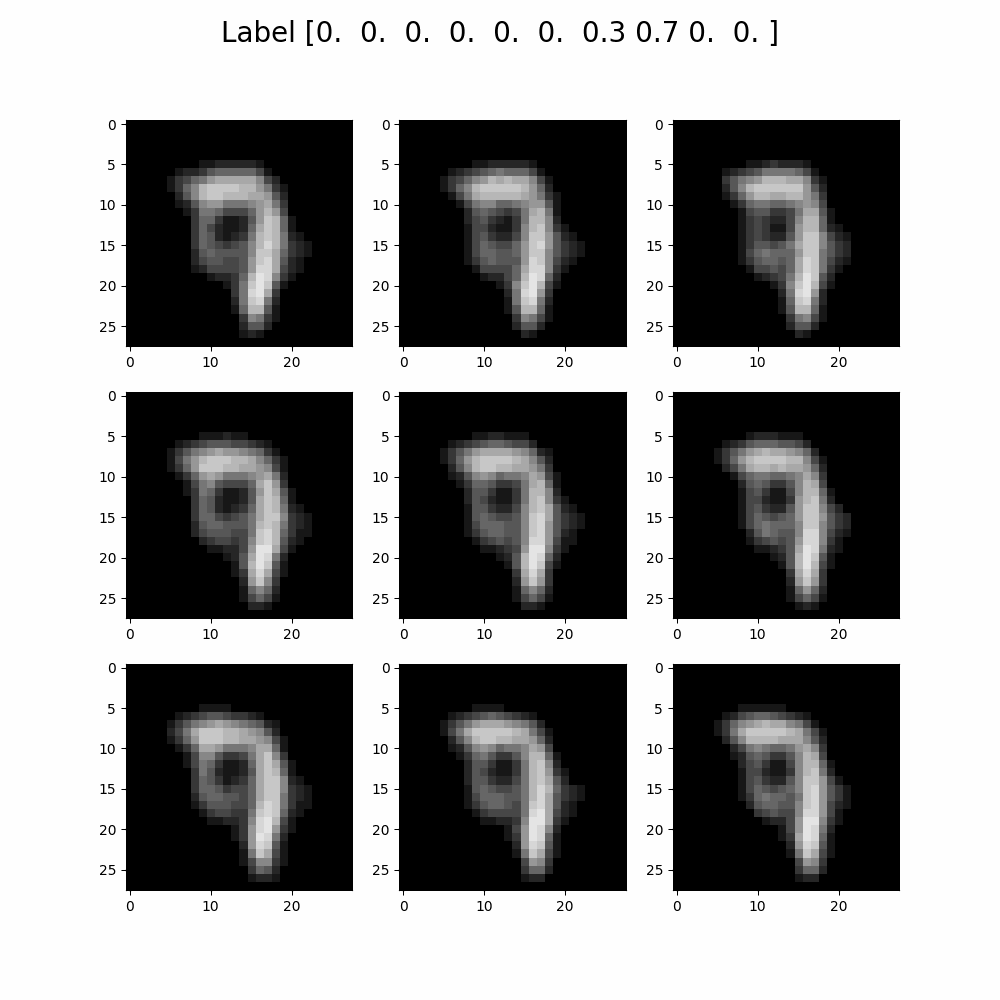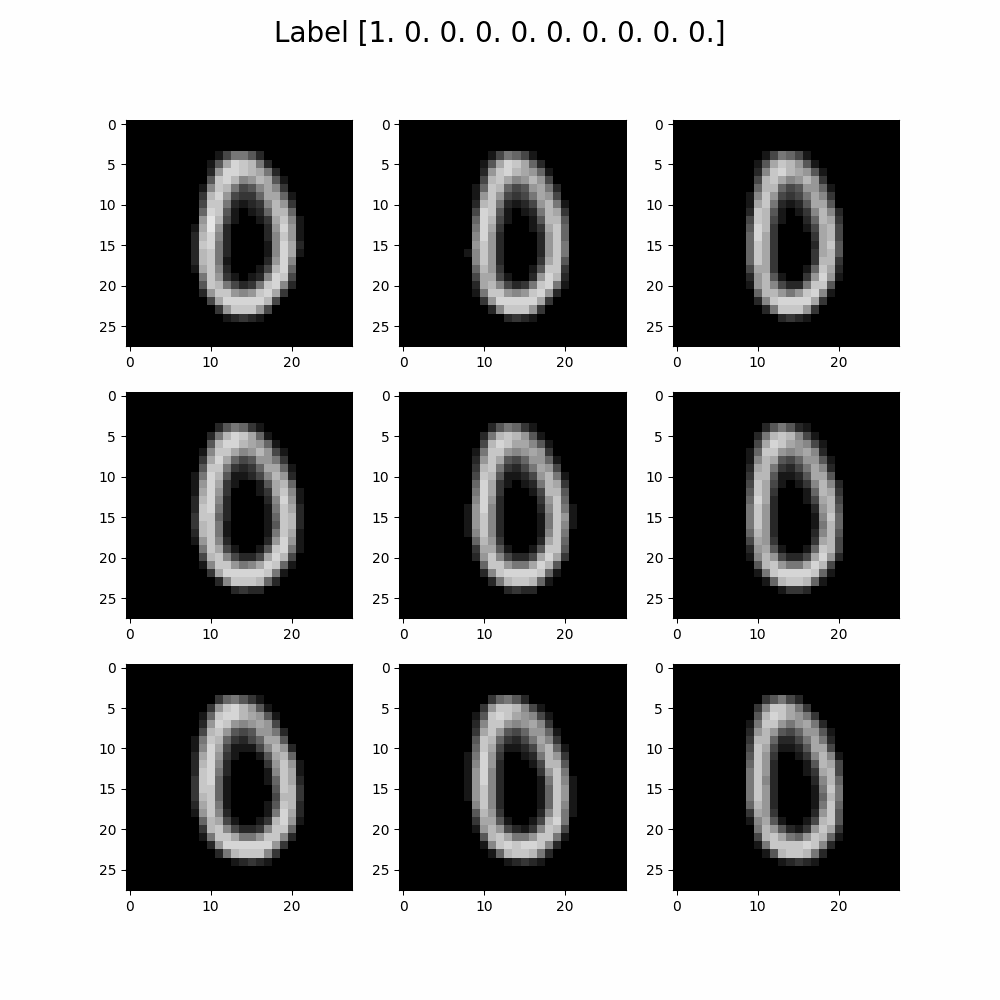
Developed a variational autoencoder which accurately reconstructs MNIST digits,
with a reconstruction loss below 135, using TensorFlow.
Implemented a latent space walk to explore the latent space of the autoencoder.
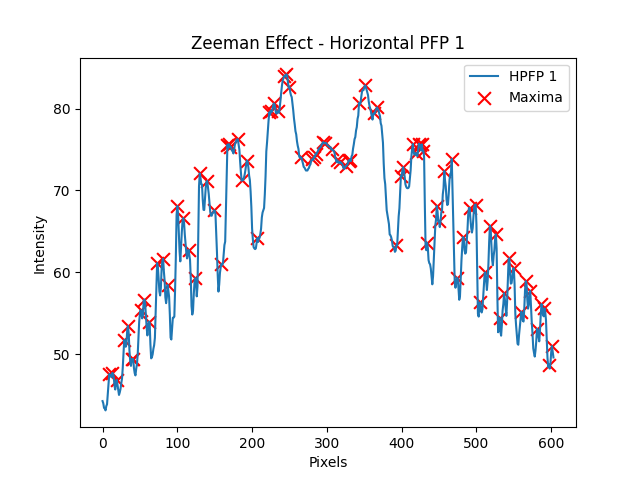
Built a program to analyse real-world lab data collected during an experiment on the Zeeman Effect.
Automates the data processing, data analysis, and statistical analysis pipeline required for this lab's work.

Get in Touch